子回路消除方法及Gurobi实现

在读研一的时候第一次接触到子回路消除这个概念，今天特意写一下相关的内容，也算是一个心得与总结，以及一些我对于子回路消除的认知与理解。本文将从一个简单的TSP问题开始讲起，提出模型与消除方法，并使用求解器Gurobi实现各种子回路消除方法。

什么是子回路？

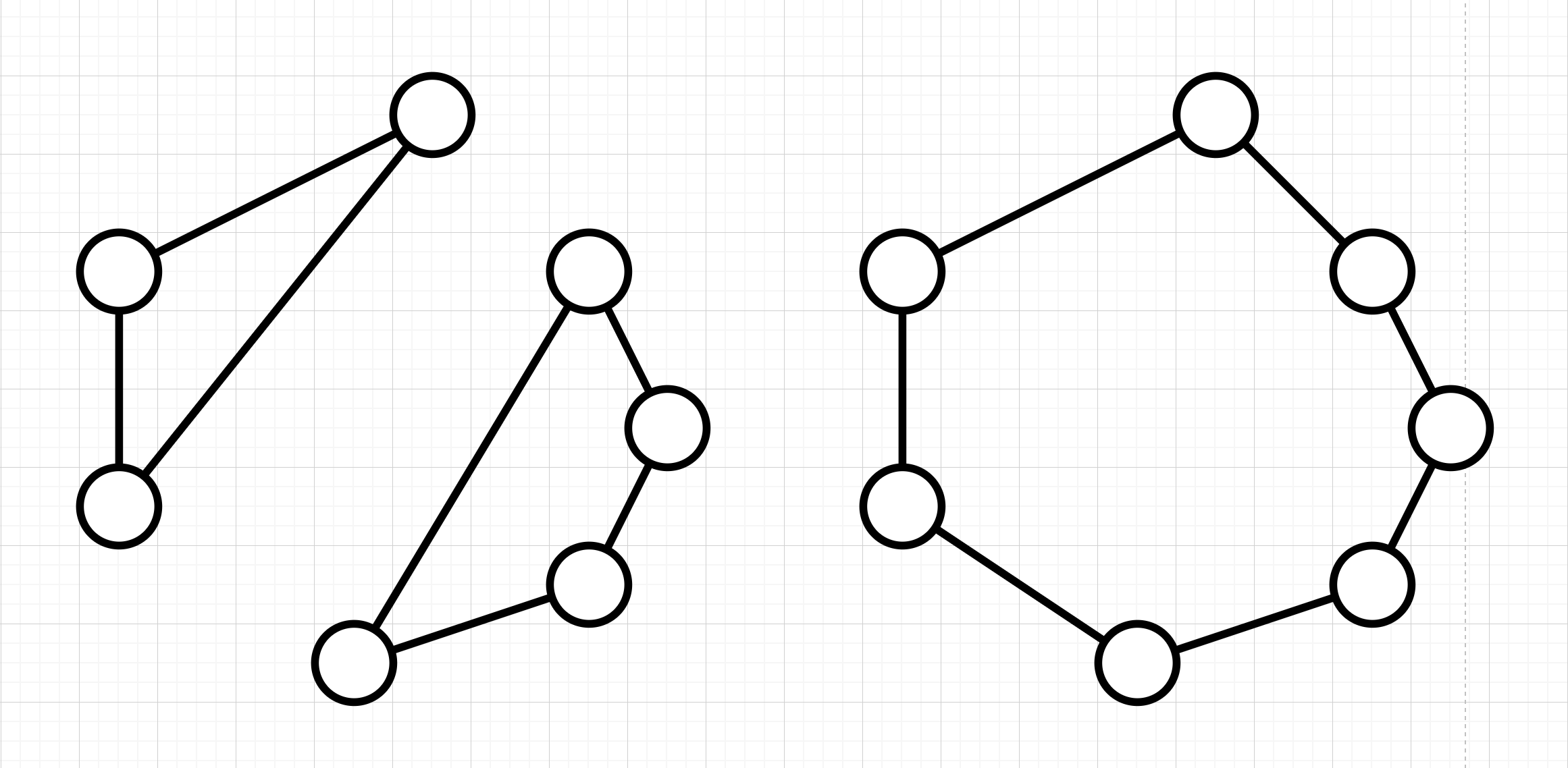
子回路是一个在TSP中和VRP中常见的现象，体现为一辆车走了两个或多个闭环路径。如果不知道VRP和TSP相关的问题与模型，建议补习相关内容。比如下面这张图的TSP问题。正常情况下，一个TSP问题的可行解应该如右图所示，即一辆车遍历所有节点。而左图中，很明显每个点被遍历了，但是竟然出现了两辆车。这显然不符合对于TSP问题的假设。然而在这种情况下（左图），两个回路竟然在数学公式上使用了同一辆车。这就是一个典型的子回路现象。

为什么出现子回路

简单来说，子回路的出现就是我们缺少一部分约束，导致没有完全地刻画问题中车辆的行为。我们知道车辆路径问题（vehicle routing problem, VRP）是旅行商问题（traveling salesman problem, TSP）问题的一个更加困难的版本，与其用一个VRP的例子作为教程，不如使用更为简单的TSP作为上手的开始。因为TSP过于经典，就不再过多赘述。简单来说就是如何以最短的距离不重复地走完地图上所有的城市并且回到出发点，其(不完整的)数学模型如下：

$$\min \sum_{i\in N} \sum_{j\in N} c_{ij}x_{ij} \tag{1}$$

$$\sum_{i\in N} x_{ij} = \sum_{i\in N} x_{ji} = 1, \forall j \in N \tag{2}$$

$$x_{ij} \in \{0,1\}, \forall i \in N, j\in N \tag{3}$$

上述公式使用了常见的符号集合，$N$是节点集合，$c_{ij}$是弧长。公式(2)表示每个点的入度等于出度，即流平衡。
公式(3)是0-1决策变量。

我们观察上面的图的左侧子图，每个点的入度也确实等于出度。也就是说上述的模型是不完整的，我们没有消除子回路的约束。

消除子回路

如上所述，我们需要增加一些约束，这些约束帮助我们消除子回路。这些约束都相当精彩，在领悟其中的原理之后拍手叫绝。

DFJ方法

Dantzig-Fulkerson-Johnson 简称 DFJ 方法是消除子回路的经典方法，公式如下：

$$\sum_{i\in S} \sum_{j \notin S} x_{ij} \ge 1, \forall S \subset N, S \ne \emptyset$$

DFJ约束规定一个节点集合$N$的非空子集$S$，要求连接$S$外面的点和在$S$内部的点的弧的数量大于等于1。换句话说，对于任意一个$N$的子集$S$，一定有一条弧离开$S$。反之，如果存在一个子集$S$，没有一条弧能够离开$S$，那就说明$S$存在子回路。

DFJ约束很简单也很直观，但是问题是约束的数量不是多项式级的，我们不太可能把一个大规模问题的所有的约束枚举出来。

MTZ方法

Miller, Tucker, and Zemlin 简称 MTZ 方法也是消除子回路的经典方法，公式如下：

$$t_i-t_j+1\leq M(1-x_{ij}), \forall i,j\in N,i\neq j$$

$$0 \le t_i \le |N|-1, \forall i\in N$$

MTZ方法引入了一个新的变量，这个变量没有任何物理意义。MTZ公式可以这样理解：
首先，如果两个点$i,j$之间存在一个弧$(i,j)$，那么两个点之间将会产生一个前后关系$i$先被访问，$j$后被访问。这个前后关系我们先假设为时间，也就是说访问$i$的时间一定比访问$j$的时间小。或者我们假设一个计数器，每经过一个点计数器增加一个单位。这个量（计数器、时间）并不存在于定义的TSP问题的物理含义中，可以解释成任意一种能够被人理解的东西（时间、计数器、容量变化…）。现在，我们用额外的决策变量代表每个点被访问的前后顺序，然后让这些值相互关联起来，就能产生前后顺序进而消除子回路。

这个额外的决策变量就是$t_i, \forall i \in N$，那么按照我们上述的计数器假设，如果点$j$在$i$之后被访问（$x_{ij}=1$），那么一定有$t_j \ge t_i + 1$。如果这种关系（点$j$在$i$之后被访问）不存在，那么$t_j \ge t_i + 1$的关系也不存在了，即$t_j$和$t_i$随意取值。我们就得到$t_i-t_j+1\leq M$，其中$M$是一个足够大的数。这样就得到了上述的$t_i-t_j+1\leq M(1-x_{ij}), \forall i,j\in N,i\neq j$的基础原理，$M$最小取值为$|N|$。

如果存在一个子回路，那$t_i$的关系是不可能成立的，因为会无限绕圈，使得$t_i$和$t_j$的关系总是不能被满足。

其他方法

在介绍了上述的两个经典的方法之后，以下是一个综述文章，介绍了各种TSP子回路消除方法。感兴趣自己看，这里就不复现了。

A comparative analysis of several asymmetric traveling salesman problem formulations,
Computers & Operations Research, 2009

Gurobi 实现MTZ和DFJ子回路消除

上述介绍中已经提到DFJ方法的约束个数是有限的，但是指数级的。我们不太可能用求解器把所有子回路的情况都考虑进去。首先声明这是一个简单的代码，用了20分钟写的简单例子，没有面向对象。

那么 talk is cheap, show me your code。

import gurobipy as gp
import math
import random
import re
from itertools import combinations

extract_numbers()从[a,b]这样的方括号中提取a和b这两个数字，并返回一个list，用于从变量名中提取索引。

def extract_numbers(s):  # 使用正则表达式匹配方括号中的两个数字
    match = re.search(r"\[(\d+),(\d+)\]", s)
    if match:
        # 提取匹配到的数字并转换为整数
        return [int(match.group(1)), int(match.group(2))]
    else:
        return None

get_tour()函数从一个字典edges中获得一个回路。字典edges的一个键值对是一条弧，键是起点，值是终点。
例如edges={1:2, 3:4, 2:3, 4:1}，则得到tour=[1,2,3,4]。

def get_tour(edges: dict):
    tour = []  # 一个回路
    while True:
        if len(tour) == 0:  # 空的回路
            if 0 in edges:  # 包含起点，则以起点开始
                tour.append(0)
                tour.append(edges[0])
                del edges[0]
            else:  # 不包含起点，则以第一个点开始
                tmp = list(edges.keys())
                tour.append(tmp[0])
                tour.append(edges[tmp[0]])
                del edges[tmp[0]]
        else:
            tmp = edges.get(tour[-1])
            if tmp == None:
                break  # 产生了一个回路
            else:
                tour.append(tmp)
                del edges[tour[-2]]
    return edges, tour[:-1]

mycallback函数为DFJ的约束添加过程，由于这样的约束数量很多无法一次添加，那么使用callback函数进行添加。
在MIPSOL处（mip solution）如果发现了一个带子回路的解，则添加针对这个回路的DFJ约束。注意，我们假设TSP的起点一定不在子回路里面，也就是只有不带起点的回路才是子回路。

def mycallback(model, where):
    if where == gp.GRB.Callback.MIPSOL:
        # 解析获得的解
        var_val = model.cbGetSolution(model._var)

        edges = {}  # TSP 决定走的边
        for i in range(len(var_val)):
            if var_val[i] > 0.5:
                tmp = extract_numbers(model._var[i].VarName)
                edges.update({tmp[0]: tmp[1]})

        # 在edges搜索一个子回路，要求起点一定不在子回路里面
        flag_subtour = False
        edges, tour = get_tour(edges)
        if len(tour) < model._node_num:  # 一定存在子回路
            flag_subtour = True

        # 针对这个子回路添加 DFJ约束
        if flag_subtour:
            edges, tour = get_tour(edges)  # 可能有多个subtour，获得一个子回路即可
            assert len(tour) < model._node_num
            # 加约束
            pairs = [(i, j) for i in tour for j in tour if i != j]
            lexp = 0
            for p in pairs:
                lexp += model.getVarByName("x[" + str(p[0]) + "," + str(p[1]) + "]")
            model.cbLazy(lexp <= len(tour) - 1)

使用DFJ方法的模型。

def solve_tsp_dfj(nodes, distances):
    # TSP 求解
    model = gp.Model()
    x = model.addVars(
        distances.keys(), obj=distances, vtype=gp.GRB.BINARY, name="x"
    )  # 变量

    model.addConstrs(gp.quicksum(x[i, j] for j in nodes if i != j) == 1 for i in nodes)
    model.addConstrs(gp.quicksum(x[j, i] for j in nodes if i != j) == 1 for i in nodes)

    model.update()
    model._var = model.getVars()
    model._node_num = len(nodes)

    # 使用LazyConstraints声明
    model.Params.LazyConstraints = 1
    model.optimize(mycallback)

    if model.Status == gp.GRB.OPTIMAL:
        edges = {}  # 被选中的边
        for i in range(len(model._var)):
            if model._var[i].X > 0.5:
                tmp = extract_numbers(model._var[i].VarName)
                edges.update({tmp[0]: tmp[1]})
        edges, tour = get_tour(edges)
        print(tour)
        print(f"路径中点的个数：{len(tour)}")
        print(f"路径长度：{model.ObjVal}")

使用MTZ方法的模型。

def solve_tsp_mtz(nodes, distances):
    # TSP 求解
    model = gp.Model()
    x = model.addVars(
        distances.keys(), obj=distances, vtype=gp.GRB.BINARY, name="x"
    )  # 变量
    t = model.addVars((i for i in nodes), vtype=gp.GRB.CONTINUOUS, name='t')

    model.addConstrs(gp.quicksum(x[i, j] for j in nodes if i != j) == 1 for i in nodes)
    model.addConstrs(gp.quicksum(x[j, i] for j in nodes if i != j) == 1 for i in nodes)
    # model.addConstr(t[0] == 0)
    node_without_starts = copy.deepcopy(nodes)
    node_without_starts.remove(0)
    model.addConstrs(
        t[i] - t[j] + 1 <= len(nodes) * (1 - x[(i, j)])
        for i in node_without_starts
        for j in node_without_starts
        if i != j
    )

    model.update()
    model._node_num = len(nodes)

    model.optimize()

    if model.Status == gp.GRB.OPTIMAL:
        edges = {}  # 被选中的边
        for i in nodes:
            for j in nodes:
                if i != j:
                    if model.getVarByName("x[" + str(i) + "," + str(j) + "]").X > 0.5:
                        edges.update({i:j})
        edges, tour = get_tour(edges)
        print(tour)
        print(f"路径中点的个数：{len(tour)}")
        print(f"路径长度：{model.ObjVal}")

主程序生成一个50个点的TSP问题，同一个问题使用两种方法求解。

if __name__ == "__main__":
    npoints = int(50)
    seed = int(41372890)

    # 创建一个随机的TSP算例
    random.seed(seed)
    nodes = list(range(npoints))
    points = [(random.randint(0, 100), random.randint(0, 100)) for i in nodes]

    # 欧式距离
    distances = {
        (i, j): math.sqrt(sum((points[i][k] - points[j][k]) ** 2 for k in range(2)))
        for i, j in combinations(nodes, 2)
    }

    for i, j in combinations(nodes, 2):
        distances.update({(j, i): distances[(i, j)]})

    # 算法求解
    solve_tsp_dfj(nodes, distances)
    solve_tsp_mtz(nodes, distances)